Full Bayesian Significance Testing for Neural Networks

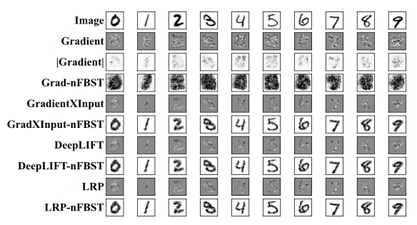
Significance testing aims to determine whether a proposition about the population distribution is the truth or not given observations. However, traditional significance testing often needs to derive the distribution of the testing statistic, failing to deal with complex nonlinear relationships. In this paper, we propose to conduct Full Bayesian Significance Testing for neural networks, called nFBST, to overcome the limitation in relationship characterization of traditional approaches. A Bayesian neural network is utilized to fit the nonlinear and multi-dimensional relationships with small errors and avoid hard theoretical derivation by computing the evidence value. Besides, nFBST can test not only global significance but also local and instance-wise significance, which previous testing methods don’t focus on. Moreover, nFBST is a general framework that can be extended based on the measures selected, such as Grad-nFBST, LRP-nFBST, DeepLIFT-nFBST, LIME-nFBST. A range of experiments on both simulated and real data are conducted to show the advantages of our method.